De Danske Cybermesterskaber: 80s Commitments
Overview
Writeup by: ChrRaz
80s Commitments
When opening http://80s-commitments.hkn we are greeted with the following page:
We are given a public key and a “commitment”. If we enter this commitment into the “reveal” box we get redirected to the following page which shows an embedded youtube video.
Refreshing the page gives a new commitment each time but keeps the public key the same.
The code
key = None
if os.path.isfile('key.txt'):
keydata = json.load(open('key.txt', 'r'))
key = ElGamal.construct(keydata)
else:
key = ElGamal.generate(1024, Random.new().read)
json.dump([key.p, key.g, key.y, key.x], open('key.txt', 'w'))
def commit_id(id):
return pow(key.g, int.from_bytes(base64.urlsafe_b64decode(id + '='), byteorder = 'big'), key.p)
flag = open('flag.txt').read()
ids = open('ids.txt').read().splitlines()
rick_id = commit_id('dQw4w9WgXcQ')
We see that the server generates an ElGamal key and stores it so the key is persistent across page visits.
@app.route('/')
def norickplz():
op = random.choice(ids)
cid = commit_id(op)
cenc = key.encrypt(cid, randint(1, key.p-1))
open('reveal.txt', 'w').write(str(cenc[0]))
return """
<html>
<body>
I commit to a lot of 80s music, but don\'t you try to rickroll me!<br/>
My public key: ({key_p}, {key_g}, {key_y})<br/>
My commitment: {commit}<br/>
Reveal:
<form method="POST" action="/reveal/">
<input name="commit"/>
<button type="submit">Reveal!</button>
</form>
</body>
</html>
""".format(key_p = key.p, key_g = key.g, key_y = key.y, commit = cenc[1])
The server loads a random youtube video id from a list and encrypts it using the ElGamal cryptosystem. It stores the first part of the ciphertext in a file for later and and gives the other part to us.
@app.route('/reveal/', methods=['POST'])
def reveal():
if request.method == 'POST':
alpha = int(open('reveal.txt', 'r').read())
beta = int(request.form['commit'])
my_id = key.decrypt((alpha, beta))
video_id = [vid for vid in ids if commit_id(vid) == my_id]
if my_id == rick_id:
return """
<html><body>
Aaah, you rickrolled me! here's the flag: {flag}<br/>
And here is the video you really wanted to see: <br/>
<iframe width="560" height="315" src="https://www.youtube.com/embed/dQw4w9WgXcQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
</body></html>
""".format(flag=flag)
elif video_id:
return """
<html><body>
Here is your cheesy 80s music video, with the tag {video_id1}:<br/>
<iframe width="560" height="315" src="https://www.youtube.com/embed/{video_id2}" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
</body></html>
""".format(video_id1=video_id[0],video_id2=video_id[0])
else:
return """
<html><body>
I'm very sorry, I couldn't find the cheesy 80s music you were looking for!
</body></html>
"""
else:
return """
<html><body>
You wanted a reveal, but what did you want me to reveal?
</body></html>
"""
When pressing the “reveal” button the server loads the first part of the ciphertext from the file from before and the other part from the input box.
If the ciphertext decrypts to dQw4w9WgXcQ then we are given the flag.
Learn ElGamal in Y minutes
An ElGamal key consists of a prime $p$, a generator $g$, a private key $x$, and a public key $y$. An ElGamal ciphertext consists of two parts which we will call $c_1$ and $c_2$. All calcuations are done modulo $p$.
When encrypting a plaintext $m$ we select a random integer $k$ from $\{ 1, \dotsc, p-1 \}$ and compute $$s := y^k,$$ $$c_1 := g^k, \text{and}$$ $$c_2 := m s.$$
To then decrypt an ElGamal ciphertext the receiver first calculates $s := c_1^x$ where $x$ is the private key. This works because $c_1^x = g^{kx} = (g^x)^k = y^k = s$. Then the receiver computes $c_2 s^{-1} = m s s^{-1} = m$ to recover the plaintext.
The attack
After encrypting a video id the server saved $c_1$ locally which means that we cannot access or modify it. However we are given $c_2$ which we can modify and send back. The server will decrypt the modified ciphertext as usual so we can pick any new plaintext $m’$ and send $c_2’ = m’ m^{-1} c_2$ in the “reveal” box. That way the ciphertext will decrypt to $$c_2’ s^{-1} = m’ m^{-1} c_2 s^{-1} = m’ m^{-1} m s s^{-1} = m’.$$
By choosing $m’$ as the id of everyone’s favourite 80’s song about commitment we are greeted with the following page:
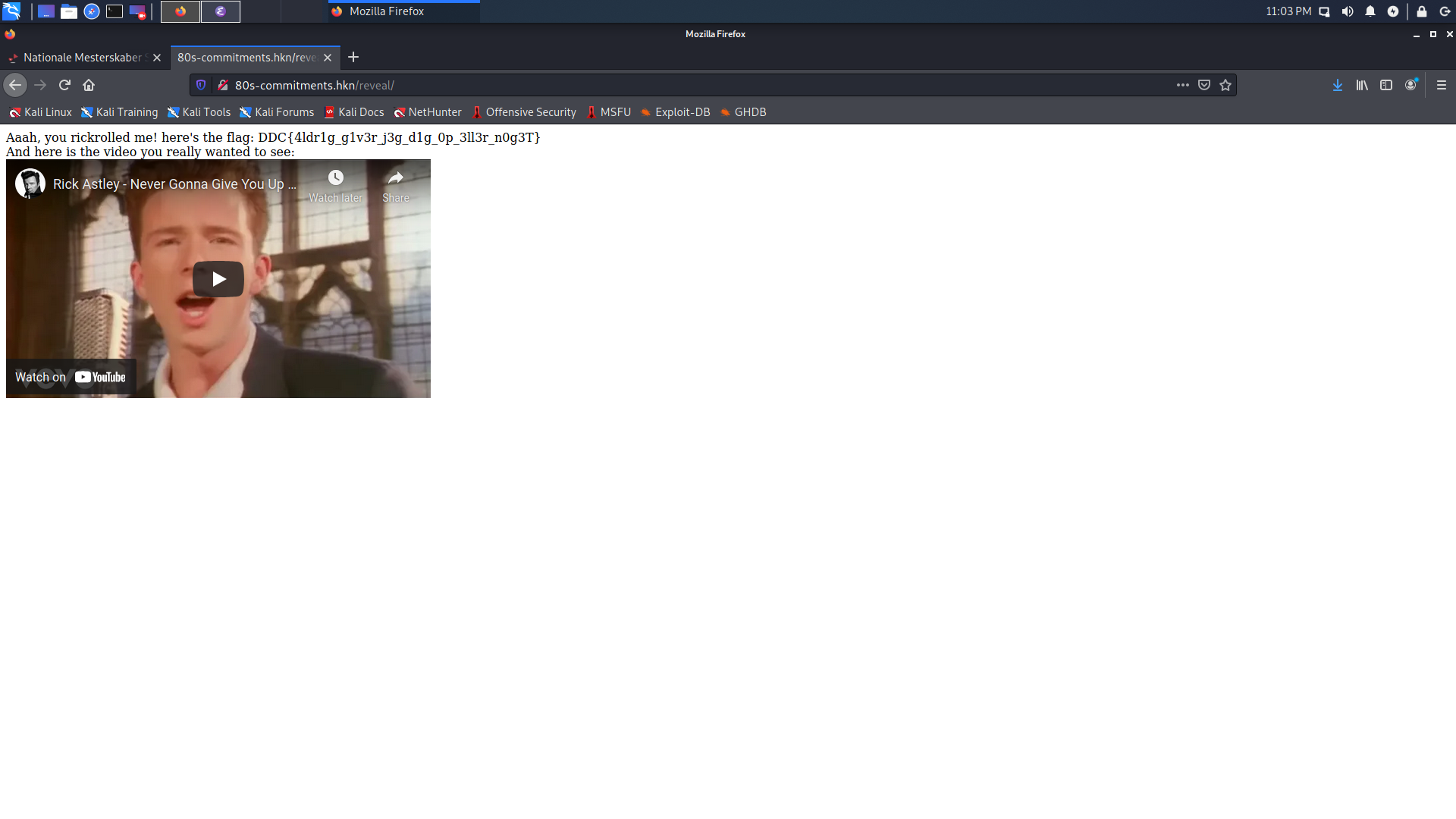
In the script below we get p, g, and y from the front page and borrow the commit_id function from the source code.
import base64
p = 171651487564665188709696071419453485395071661478962815543726294106018240905063215109668595489789996605360205665709272203829586629878234979355953282462961745069389037545035054232207660340222173839586890685127419728129664935083084059915287590870642102026331366475529208457259452436612905460819402026975569601899
g = 27305933566818278720696389534012959492649387746252108251770409919396275174057176634224305878634581806277044720415849682636085818092615674889056390082015679654921658340400858196943671854522774982673668016420578497559718448965162949499550758735528210054243289575125149360586547518514288700022584365578504751595
y = 145090189738016153466490236476054801168926982849349017938207186794937966980007538982216686590226014219884866993390684044683881069330459447210806092392186443363786007847558108514944678055845610290490448691643407244158338140702203311968595785050042203456855729948131551519672953984421021457758139828574059447101
def commit_id(id):
return pow(g, int.from_bytes(base64.urlsafe_b64decode(id + '='), byteorder = 'big'), p)
rick_id = commit_id('dQw4w9WgXcQ')
url_id = commit_id('oDnNF5cHCdo')
commitment = 8749597161297144944347262743580131683611775850149009785197715835761728714425049524644578101598581339940416246251159461674069450938784967399443411632278085435621252421883882740550319011403258543616787447073968856680053821648005449632376328675021457879848545252373577678340725820429124832527973618762264039066
new_commitment = (commitment * pow(url_id, -1, p) * rick_id) % p
print(new_commitment)
Alternatively, because any good crypto writeup has to include some Sagemath code:
import base64
p = 171651487564665188709696071419453485395071661478962815543726294106018240905063215109668595489789996605360205665709272203829586629878234979355953282462961745069389037545035054232207660340222173839586890685127419728129664935083084059915287590870642102026331366475529208457259452436612905460819402026975569601899
F = GF(p)
g = F(27305933566818278720696389534012959492649387746252108251770409919396275174057176634224305878634581806277044720415849682636085818092615674889056390082015679654921658340400858196943671854522774982673668016420578497559718448965162949499550758735528210054243289575125149360586547518514288700022584365578504751595)
y = F(145090189738016153466490236476054801168926982849349017938207186794937966980007538982216686590226014219884866993390684044683881069330459447210806092392186443363786007847558108514944678055845610290490448691643407244158338140702203311968595785050042203456855729948131551519672953984421021457758139828574059447101)
def commit_id(id):
return g ^ int.from_bytes(base64.urlsafe_b64decode(id + '='), byteorder = 'big')
rick_id = commit_id('dQw4w9WgXcQ')
url_id = commit_id('oDnNF5cHCdo')
commitment = F(8749597161297144944347262743580131683611775850149009785197715835761728714425049524644578101598581339940416246251159461674069450938784967399443411632278085435621252421883882740550319011403258543616787447073968856680053821648005449632376328675021457879848545252373577678340725820429124832527973618762264039066)
new_commitment = commitment / url_id * rick_id
print(new_commitment)